 |
 |
 |
Science at the Crossroads by Herbert Dingle Select Quotations [CG addenda in blue text; page numbers refer to the pdf here] |
 |
 |
 |
Part Two - The Intellectual Issue |
Chapter 6 - Four Outstanding Errors
I think it will be helpful to pinpoint four basic misunderstandings, an awareness of which will make it easier to understand why special relativity has been accepted for so long in spite of its clear untenability. They are concerned with - first, the relation between mathematics and physics; second the confusion of different meanings of the word 'time'; third, the misinterpretation of 'co-ordinate systems' as 'observers'; and fourth, what I can best describe briefly as the literal interpretation of metaphors - the acceptance, as direct observations, of what are actually remote implications of possibly erroneous theories. [p.83]
Take, for example, the simple mathematical equation, 1+1=2. Over a wide range this holds good in experience as well as in mathematics, where it is always true. If we have one penny, and someone adds another to our wealth, we have two pennies. If we have one apple and add to it another and count the total, we find that it is two apples. And so on. We may therefore be inclined to generalise, and say that if we add one anything to another of the same thing, we have two of those things; in other words, x+x=2x, whatever x may be. But this is far from the truth. If we add one water drop to one water drop we get not two water drops but one larger drop. [p.86]
Examples could be multiplied ad lib, but I think these are enough to show how general and how dangerous is the prevailing illusion that all that is necessary to entitle a physical theory, however absurd, to respect is to discover some mathematical process whose symbols can be arbitrarily correlated with the physical entities of the theory, without regard to evidence or probability or commonsense. We shall see in due course that the supposed justification of special relativity by the 'mathematicians', to whom the 'experimenters' entrust it, lies wholly in the impeccability of its mathematical structure: the impossibility of the application to experience of that structure, in the manner postulated by the theory, is left out of consideration altogether .... [p.87]
I think it is impossible for anyone who reflects on the few examples I have given, and realises that they are not exceptional in their general character but typical of most mathematical physics of the present day, to doubt that, as a general rule, the practice of mathematical physics goes hand in hand with lack of elementary reasoning power and of that normal form of human wisdom, somewhat misleadingly called commonsense, that provides its own corrective of premature judgement and never allows the requirements of reason and experience to be overcome by the seductions of attractive speculations. I repeat that I am no psychologist, and it is with diffidence that I admit an unwillingness to conclude that this is an inescapable psychological necessity; it is more comforting to hope that it denotes a failure of our educational system to recognise an ever-present danger and to take precautions against it. [p.87]
Dingle contrasts mathematical ability with intelligence or common sense (or "human wisdom" as Dingle prefers to call the latter, but he might also have said "logic") making a clear distinction between them. Note that by "mathematical ability" Dingle is referring in particular to what might be described as a kind of intuitive divination of the possibilities and solutions of abstract equations, rather than the more commonly held notion of mathematics, which is chiefly arithmetic and algebra. (Arithmetic, of course, is certainly a part of common sense.) Dingle's comparison of mathematical divination to the ability of a proficient chess player (another ability commonly and mistakenly believed to be necessarily associated with intelligence) is particularly insightful. (Remarkable chess ability has more to do with a kind of intuitive spatial awareness than anything else.) In fact Dingle is making a similar distinction to the one Plato makes in "The Republic" between cookery and chemistry (for example), the former, according to Plato, being more akin to a "knack" than an exercise in logic and reason.
It is usually taken for granted that the processes of mathematics are identical with the processes of reasoning, whereas they are quite different. The mathematician is more akin to a spider than to a civil engineer, to a chess player than to one endowed with exceptional critical power. The faculty by which a chess expert intuitively sees the possibilities that lie in a particular configuration of pieces on the board is paralleled by that which shows the mathematician the much more general possibilities latent in an array of symbols. He proceeds automatically and faultlessly to bring them to light, but his subsequent correlation of his symbols with facts of experience, which has nothing to do with his special gift, is anything but faultless, and is only too often of the same nature as Lewis Carroll's correlation of his pieces with the Red Knight and the White Queen - with the difference that whereas Dodgson recognised the products of his imagination to be wholly fanciful, the modern mathematician imagines, and persuades others, that he is discovering the secrets of nature. [p.87]
The processes of mathematics are to be contrasted rather than identified with the process of rational thought. [p.88]
.... mathematical ability and ability to conduct operations of thought are distinct faculties, and although I know of no reason why they should not co-exist in the same person, it is only too clear that at the present time, except in a rare instance, they do not. [p.88]
Government now demands, above all things after moral rectitude, intelligent thought, and it must be recognised that mathematical physicists are, of all our citizens, the least fitted to provide it. [p.88]
‘To the scientist,’ writes Professor (now Sir) Fred Hoyle, ‘war starts because human behaviour is representable in terms of mathematical equations possessing discontinuous solutions.’ This must not be dismissed as a humorous wisecrack: Hoyle, and others of his type, really believe that this is so. They were not necessarily born with a deficiency of commonsense: they have exceptional mathematical ability, which has been mistaken for exceptional intelligence, and have been so trained that their normal intelligence has expired through desuetude; much mathematics hath made them - what they are. They are now no more able to perceive the advantages of intelligence than the blind men in H. G. Wells's story could perceive the advantages of sight. [p.88]
Dingle discusses the misapplication of the mathematical language to Science in recent times and its "mastery, instead of servitude in relation to physics":
As we have seen, Galileo - who, more than any other single person, can be regarded as the originator of modern physical science - claimed that the book of nature was written in the mathematical language. He meant exactly what he said: mathematics was a language, a means of expressing something, not the thing that it was important to express. Both Galileo and Newton took experiments or observations as their starling-point, and used mathematics only as a tool to extract the maximum amount of knowledge from the experiments and as a means of expressing that knowledge. [p.89]
Of course, there are numerous instances in which mathematics has suggested physical possibilities which have later been realised and might not have been thought of without the suggestion; its service in this respect can hardly be over-estimated. [p.89]
.... so far as I have been able to discover, the first serious example of the mastery, instead of the servitude, of mathematics in relation to physics came with Maxwell's theory of the electromagnetic field, and that, as would be expected, only in a very tentative way and not without resistance. In brief, Maxwell showed that Ampere's law in electromagnetism, expressed mathematically - which, of course, as I have said, was a mathematical expression of results found by experiment - did not satisfy the equation of continuity but could be made to do so by a purely mathematical modification. Accordingly he assumed that this modified form was the actual physical law. But he was too conscious of the true relation between mathematics and physics not to be aware that this was quite unjustifiable unless an actual physical relation existed which was represented by his proposed equation; and since he knew of none, he made the assumption that what he called a 'displacement current' existed in a dielectric. The physical feature that distinguishes a dielectric from a conductor is that the latter, but not the former, can convey an electric current, so this was quite inadmissible on observational grounds, but Maxwell assumed that a 'displacement' of electricity could occur in a dielectric, which had the same physical effects, so far as these were required by the equations, as a current in a conductor. [p.89]
Dingle cites German physicist Heinrich Hertz's opinion of Maxwell's theory:
'To the question, "what is Maxwell's theory?" I know of no shorter or more definite answer than the following: — Maxwell's theory is Maxwell's system of equations.' [p.90]
.... a state of mind was generated in physicists by which, while still formally adhering to the principle that observation was basic and mathematics a useful tool, they were ready to accept mathematical requirements as an adequate substitute for a genuine theory, even though they could see nothing intelligible that corresponded to it physically. It was a short step from acceptance of the physically unintelligible to the physically absurd, but the description of this must be postponed until we come to the origin of the special relativity theory itself. [p.90]
On the confusion caused by multiple meanings of the word "time" as it is often used in expositions of special relativity theory:
I pass now to the second of the general considerations previously mentioned, that help us to understand the confusion and misconceptions that surround the word 'relativity': it is the multiplicity of meanings associated with the word 'time'. If it is the misconception of the relation between mathematics and physics that is chiefly responsible for the belief that special relativity is physically true, this second confusion is chiefly responsible for the widespread conviction that it is an esoteric and difficult subject and indeed anything but a rather simple physical theory of the well-understood traditional kind. [p.92]
Now what will probably surprise many readers is that Einstein's special relativity theory, as he expounded it in his 1905 paper, has nothing at all to do with time in the sense of 'eternity'; it is concerned only with instants and durations (as intervals between instants). [p.93]
.... time, in Einstein's theory as in physics generally, means only clock-readings. It is because of this confusion that the 'experimenters' have left relativity to the 'mathematicians'. Their concern has been only with what can be the subject of observations, and 'eternity' cannot be observed; it can only be thought about, and the 'experimenters' leave that kind of thought to mathematicians and philosophers. These draw deductions about 'eternity', and pass them on to the 'experimenters' as relating to 'instants' and 'durations'. They are accepted as such, without understanding but with blind trust. The reader may foresee what will ensue, if this process is allowed to continue. [p.93]
The achievements of physics - the establishment of relations between measurements of various kinds - are summed up in a number of equations, in which the symbol t occurs with great frequency, but never with the meaning of 'eternity'; it always means an 'instant' (i.e. directly or indirectly a clock-reading) and t2 - t1 means a 'duration'. [p.93]
When once the distinction between eternity, instant and duration is recognised, the general literature of the subject of relativity is seen to be in utter confusion. The writer, quite unaware that the word 'time' has different meanings, unconsciously oscillates between them, and the reader, equally unconsciously, becomes the victim of one non sequitur after another, in which he can see no failure of reasoning but yet no possibility of making sense of the conclusion: thus is generated the illusion that relativity is incomprehensible to the ordinary mind. [p.94]
Einstein's theory was designed to provide a relation that held for both kinds of events. [i.e. mechanical and electrodynamical] It was wholly physical, and concerned wholly with a problem of the traditional kind, involving only traditional concepts. We shall see later how, through the delayed action of Minkowski's metaphysical interpretation of his own mathematics, it came to be enveloped in a metaphysical cloak that had nothing whatever to do with its essence. [p.95]
Dingle discusses the conflation of "observer" and "co-ordinate system" in special relativity terminology, and the resultant confusion:
All science is based on observation, and whatever we say about the world studied in science must justify itself ultimately in terms of what we actually observe, not of what we infer that hypothetical observers would experience in circumstances impossible yet to attain. Now effectively, in all matters with which special relativity is concerned, there is only one observer - a terrestrial one - for the relative motions possible to terrestrial observers are so small as to be negligible in this connection. Hence the theory must be wholly expressible in terms of the experiences of that one observer alone. [p.96]
.... all phenomena generally associated with relativity - relative contraction of rods, relative slowing down of clocks, etc. - are not matters of observation but are wholly concerned with co-ordinate systems, and the essential difference between an observer and a co-ordinate system is that the same observer (and we have seen that there is effectively only one observer in the universe on whose observations all the science we have yet achieved can be based) can choose any of an infinite number of co-ordinate systems that he pleases (provided that in special, though the limitation does not exist in general, relativity their relative motion is uniform). [p.96]
In laboratory experiments we usually choose a system in which the Earth is at rest. In dynamical astronomy we choose one in which the Sun is at rest and the Earth moving at 18 ½ miles a second. In stellar astronomy we choose one in which the Earth is moving round the Galaxy at a few hundred miles a second. And so on. Clearly, nothing whatever that we observe is changed by our change of mind. [p.97]
[Special Relativity] is all concerned with the change of values which a single physicist must make in the coordinates he assigns to objective events when he decides to change his co-ordinate system. What he observes will change no more than what we observe will change when we stop thinking of ourselves as resting in bed and reflect that we are moving round the Sun. The changes in the co-ordinates, however, will be different from those believed to be necessary before the theory was devised, and it is on these differences alone that the theory must be judged. [p.97]
Dingle compares Lorentz theory with special relativity theory declaring them mathematically indistinguishable yet nonetheless fundamentally different in terms of physical basis. A key difference is that the Lorentz theory does not do away with the ether.
.... all the supposed experimental verifications of special relativity can with exactly the same justification be advanced as verifications of Lorentz's earlier and quite different theory which is described in Chapter 8. This is so because both theories have the same mathematical structure and give indistinguishable physical interpretations to the symbols involved so far as the experiments so far performed are concerned, though there are quite irreconcilable differences of interpretation between which it is not yet possible to decide — or at least between which no existing experimental knowledge can decide, though I think the necessary knowledge would be obtained readily enough if there were a sufficient appreciation of the fact that special relativity is still possibly open to doubt. [p.97]
Dingle makes an important point about the metaphorical nature of our "knowledge" of sub-atomic particles:
.... what do we mean when we speak of the mass of an electron? We certainly do not put an electron in a balance pan and compare it with weights in the other pan. We could not do so because not only can we not capture an electron but also we do not know what it is .... Eddington probably gave it the most candid description as 'something unknown doing we don't know what'. We are no wiser today; nevertheless, we speak of the mass of an electron as though it was equivalent to the mass of a lump of lead. [p.98]
On the circular argument inherent in attempts to prove the predictions of special relativity or Lorentz's theory with experiments involving "hypothetical" particles:
.... the whole complex of conceptions that yields the highly metaphorical 'mass' and 'velocity' hangs together if we include special relativity (or Lorentz's theory) as a part of it. This would indeed argue in favour of one of those theories if that theory were independent of the previously existing complex of conceptions, for our object in physics is to relate apparently independent phenomena in a single system, but when the theory (Lorentz's or Einstein's) is conceived for the purpose of justifying an essential part of that complex - to wit, the Maxwell-Lorentz theory - it proves nothing at all. It is like claiming, as a proof that a man always speaks the truth, the fact that he says he does. [p.98]
On "short lived mesons in cosmic rays" (otherwise known as mu-mesons or muons) that are commonly held by relativists to be proof of special relativity:
We shall see that this is precisely the case with this (and indeed every other) supposed confirmation of special relativity involving hypothetical particles. Einstein, as he said, designed his theory to conform to the Maxwell-Lorentz electromagnetic theory which he accepted as equivalent to 'certain'. All that the supposed confirmations support is therefore the fact that special relativity was well designed for its purpose. They tell us nothing whatever about the truth of either electromagnetic theory or the special relativity (or Lorentz's) theory itself. An example of the illusion that they do that we have already met is that advanced by Sir Lawrence Bragg concerning cosmic rays and expressed in the usual jargon in the editorial in Nature in the words, 'short-lived mesons in the cosmic rays appear to observers on the surface of the Earth to last long enough to reach the ground'. It needs not saying that the duration and distance of their fall are not measured by a stop-watch and measuring-tape but are first inferred from a course of reasoning that includes the original Maxwell-Lorentz theory, and is then 'corrected' by the special relativity theory designed for the purpose of correcting it. Is it surprising that the answer comes out right? [p.99]
It is impossible to believe that men with the intelligence to achieve the near miracles of modern technology could be so stupid as to fall into this elementary error had they not, through long familiarity with the words, unconsciously come to believe that mass, time, distance, and such terms mean the same for hypothetical particles as for the world of the senses. Physicists have forgotten that their world is metaphorical, and interpret the language literally. I do not think Einstein would for one moment have regarded these cosmic ray observations as evidence for his theory, but only as an application of it. His theory in itself was wholly kinematical: it corrects electromagnetic theory because it created a new kinematics for that end; it can therefore be tested only by straightforward kinematics with sensible bodies, and by reasoning in which the words used have their literal, and not their metaphorical, meanings. [p.99]
These four matters - the relation between mathematics and physics, the confusion of meanings of the word time, the mistaken identification of co-ordinate systems with observers, and the literal interpretation of metaphors - are, I believe, the chief sources of the misunderstanding of the theory and, above all, of the illusion that it is in any way more esoteric or mystical or generally unintelligible than any other department of physics. It is, on the contrary, a rather simple theory - far simpler than Maxwell's theory of electromagnetism, or thermodynamics, for example. It is no more difficult than the first principles of Newton's kinematics; indeed, the two systems are on a par with regard to practically every feature - they are alternative systems of kinematics, i.e. of the fundamental relations between motion and the readings of measuring rods and clocks .... They can therefore appeal to nothing more fundamental, but each must justify itself on grounds of pure reason allied with experiences so simple as to be unquestionable. [p.99]
On Einstein's arbitrary redefinition of the time of an event at a distance:
.... Newton's kinematics assumed that the time of a distant event was that shown by a clock at the place of that event, that had been synchronized with a terrestrial clock when adjacent to it and then moved at a uniform speed to that place.
Lorentz, as we shall see, was the first to challenge that assumption, by postulating that motion of the clock through the ether changed its rate; but Einstein, discarding the ether, fell back on the fact that it was an assumption that a distant event had any unique instant of occurrence at all (or, to put it in another way, if one spoke of the time (instant) of a distant event, it was necessary to give the word a meaning, and one was free to choose the meaning). In the absence of any self-evident, necessary way of determining such an instant, Einstein claimed the right to define it in such a way as to save the electromagnetic theory without violating the principle of relativity of motion. Furthermore, he succeeded in discovering such a definition. [p.100]
.... it is most important to notice this. Einstein had not disproved Newton's implied requirement that the rate of a clock was not affected by uniform motion; he had only shown that it was not a necessary requirement, and that, in the absence of evidence to the contrary, any other self-consistent assumption about the effect of motion on the rate of a clock was permissible. It is because the assumption which he made has been believed to be self-consistent - and, still more effectually, because, if it is, it does save the electromagnetic equations and make them accord with numerous electromagnetic observations that have been made since (including, for example, the cosmic ray phenomena cited by Sir Lawrence Bragg), that Einstein's theory has succeeded in displacing Newton's. The criticism of Einstein's theory made here is that his assumption is, after all, not self-consistent because it requires each of two clocks to work steadily faster than the other, which is clearly impossible. [p.100]
The way is now clear for a description of Einstein's theory and an account of the circumstances that have led to the remarkable oversight of what is, in fact, a very simple defect. This I now propose to undertake. The one thing necessary - and it is absolutely essential - is the abandonment of the now almost instinctive conviction that there is anything mysterious in the whole thing, and the recovery of trust in elementary reasoning and commonsense. If that can be achieved the rest is simple. [p.101]
Chapter 7 - Einstein's Theory in its Original Context
It was quite otherwise in electromagnetism. An electric charge at rest was surrounded only by an electric field, but an electric charge in motion was equivalent to an electric current and was surrounded by a magnetic field also. There was thus an observable physical difference between the two cases, so that motion in electromagnetism was not merely relative - the motion of one body with respect to another - but absolute - something that had detectable consequences quite irrespective of any visible standard of rest to which the motion could be referred. But since the very idea of motion implied such a standard, an invisible universal medium - the ether - was regarded as acting in this capacity, and, this, as we have seen, was made by Maxwell the basis of his theory and the indispensable physical medium for conveying light and electric waves. [p.103]
Indeed, the velocity of a material body through the ether could be determined by measuring its velocity with respect to light; for light, according to Maxwell's theory, was an electromagnetic phenomenon having a known constant velocity through the ether. Nevertheless, delicate experiments based on Maxwell's theory - of which the famous Michelson-Morley experiment was the chief - failed to detect any difference at all between the velocities, with respect to light, of bodies that were known to be moving with respect to one another. [p.103]
Dingle does not question here the Copernican model of the universe, which might also have been called into question by the Michelson-Morley results, though elsewhere he notes regarding special relativity theory: "Science no longer refuses to tolerate the neglect of any anomaly; it refuses to tolerate anything but neglect of a most outstanding anomaly. It no longer fears only prejudice and preconception; it fears to the point of terror a particular threat to its prejudices and preconceptions, and does everything in its power to suppress such a threat. Its criteria of truth - if that word can still be used in connection with it - are no longer reason and experience, but strict conformity to a theory that, despite its apparent successes, is still less plausible and less supported by observation than, in their day, were Ptolemaic [geocentric] astronomy and Newton's law of gravitation, both of which are now, rightly or wrongly, out of fashion." [p.74]
I shall now attempt to describe what Einstein did in his 1905 paper, and show, I hope, that, although it was revolutionary and profoundly original, it was in no degree at all esoteric, mystical, metaphysical, or in more than a very elementary way mathematical, but was and is wholly intelligible to any normal person acquainted with the rudiments of traditional physics. Its reputation as the supreme model of the incomprehensible is wholly spurious. [p.104]
Einstein's ultimate aim, of course, was to reconcile kinematics with electromagnetism, and his method of approach differed from that chosen almost automatically by others in that it proposed a modification of kinematics rather than of electromagnetism for this end. This was its most distinctive feature, and so little is it still understood that .... it is still thought by most physicists that the theory can be vindicated by electromagnetic experiments. Since it was essentially and quite openly expressed as a reform of kinematics made for the very purpose of explaining such experiments, it can be tested only in kinematical terms. [p.104]
Einstein divided his paper into two parts, which he called 'I. Kinematical Part'; 'II. Electrodynamical Part'. The whole essence of the theory is contained in the former, on which, for the reason stated, I should concentrate attention. If that is right, the rest follows without question; if it is not, its application to all electromagnetic phenomena, of whatever kind, is worthless, despite the profound impression it has made on the 'experimenters'. [p.104]
[Einstein's] weakness, as we shall see, lay in his relative inability to follow up the implications of his insight and in a too great readiness to accept a promising starting-point as an achieved goal. He was rather like one of a body of men imprisoned in a dungeon, who alone perceives an opening offering a means of escape, but omits to verify that it does not lead merely to another part of the dungeon. [p.104]
What Einstein was proposing, therefore, was to retain the finite velocity of light without the existence of any standard with respect to which that velocity had a meaning. Light consisted of waves, with a definite length, frequency and velocity, in nothing; it was the grin without the Cheshire cat. [p.108]
If the velocity of light was finite, and there was no ether with respect to which it had that finite velocity, the only apparent alternative was that each beam of light had that velocity only with respect to its own source, and this the theory denied. However, apparent contradictions were at a discount, but what the two postulates, taken together, did imply was that the time (instant) of a distant event had now to be granted an infinite number of different values, all equally 'right'. [p.109]
Einstein was justified in freely choosing a definition of distant times (instants), provided that he then meant by 'time' only what the definition required. He was not justified in supposing also that time (instant) was what the previously accepted instruments called clocks would record in prescribed circumstances, unless experiment showed that that was so, and the necessary experiment was, and still is, impossible for practical reasons. His theory, in fact, consisted in the postulate that clocks would, in fact, give readings that accorded with his definition.[ p.110]
.... the theory is wholly kinematical, electromagnetism having nothing to do with it. It does introduce light, but only as something having a velocity; the nature of light does not enter the theory at all .... the theory itself is wholly kinematical, and stands or falls by kinematical considerations alone. As I have repeatedly said, none of the supposed electromagnetic experiments and observations (including those connected with cosmic rays/can possibly do more than show that if the theory could be right, it would achieve its purpose, it would provide an effective correcting factor to the electromagnetic equations. But such experiments and observations, individually or collectively, are, as evidence for the truth of the theory, completely valueless. [p.111]
Chapter 8 - Non-Einsteinian Relativity
To put the matter in a nutshell, an unelectrified rod at rest, according to the ideas of the time, consisted of equal quantities of positive and negative electricity in some form or other. When the rod was set in motion, these charges became two parallel currents of electricity in opposite directions, and such currents were known to repel one another. Accordingly, there was a force increasing the breadth of the longitudinal arm (which did not affect the path of the light) and the length of the transverse arm. Hence the FitzGerald effect was not a contraction of the former but an expansion of the latter. [p.114]
Lorentz formulates the mathematical fix known as the "Lorentz transformation" which transforms also the time co-ordinate. Einstein would use the same mathematics for his own theory published in a paper the following year:
.... independently of this and in ignorance of it, Lorentz in 1904 proposed a much more comprehensive theory which, if valid, not only explained the null result of the Michelson-Morley experiment but provided a supplement to the Maxwell theory which implied that any experiment with material systems, carried out on bodies moving uniformly with respect to one another, would give exactly the same result, so that it would be inherently impossible to tell, from an experiment confined to a body, whether that body was at rest or moving uniformly through the ether. His proposal was that motion of a material body through the ether produced a contraction in the direction of motion, and a slowing down of all rhythmical processes, both by the factor (1 – v2/c2)1/2, where v was the velocity of the body and c the velocity of light. Lorentz showed that if these physical effects were a reality, the relation between the co-ordinates, (x, t) of an event referred to one system, and the coordinates, (x', t'), of the same event referred to a system moving uniformly in the direction with respect to the first (for simplicity we consider one direction only - that of the relative motion - and suppose certain initial conditions to be satisfied) was given by the equations
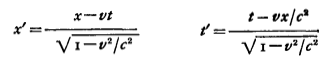
Mathematically their significance lies in the fact that, in mathematical language, the equations of the Maxwell-Lorentz electromagnetic theory are invariant to them; that is to say, if, for x and t in those equations, we substitute the values given by the Lorentz transformation, we obtain identical equations with x', t' taking the places of x, t, and v changing to - v. This guaranteed that all measurements made on either of two bodies, in uniform relative motion with velocity v (or - v), when interpreted in terms of the Maxwell-Lorentz theory, would be related in the same way, so that no physical observations confined to either of the bodies could distinguish the motion of that body from the motion of the other. It would still be possible, of course, by comparing observations on the two bodies, to detect effects of their relative motion, but experiments such as that of Michelson and Morley, for example, which were confined to the Earth, could not reveal the motion of the Earth. [p.114]
Dingle explains the chief difference between the Lorentz theory and Einstein's special relativity, in particular that Lorentz at least tried to offer a physical explanation for his transformations whereas Einstein made no attempt to explain how light could have the properties of an electromagnetic wave without a medium to travel in (i.e. the ether):
Nevertheless, [the Lorentz theory] was a physical theory, not a mathematical one; that is to say, the proposal was that motion through the ether produced physical effects on bodies, and the mathematics expressed the physical results produced. Like Maxwell, who realised the necessity, if he was to satisfy his mathematical desires, of postulating a 'displacement current' to justify them, so Lorentz, in order to justify his transformation equations, saw the necessity of postulating a physical effect of interaction between moving matter and ether, to give the mathematics meaning. Physics still had de jure authority over mathematics: it was Einstein, who had no qualms about abolishing the ether and still retaining light waves whose properties were expressed by formulae that were meaningless without it, who was the first to discard physics altogether and propose a wholly mathematical theory. [p.115]
Lorentz's theory does not include any explicit constraints on the speed of light:
Moreover, Lorentz entitled his paper, 'Electromagnetic Phenomena in a System moving with any Velocity less than that of Light' - thereby implying that, unlike the later theory of Einstein, his proposal did not prohibit velocities of systems greater than that of light. [p.115]
Lorentz's theory demands an ether, and therefore, though mathematically equivalent to special relativity theory, is not itself, strictly speaking, a relativity theory:
Strictly speaking, the name 'relativity theory' should be applied only to a theory that regards motion as a purely relative phenomenon - i.e. a theory that, like Einstein's, allows no ether. Lorentz's theory demanded an ether. He, and the great majority of his contemporaries, never doubted the physical reality of the ether, as something that both had physical properties and could serve as a standard of rest with respect to which 'absolute' velocities had a definite meaning. [p.115]
It is important to notice that, on Lorentz's hypothesis, it would still be possible to detect motion through the ether if velocities so high that terms of higher order than the second became significant were attained. Though this was, and is, practically impossible, it affords a theoretical distinction between the requirements of the theories of Lorentz and Einstein, which both include the Lorentz transformation. [p.115 footnote]
The general effect, however, of Lorentz's theory was one of acceptance. It received the powerful support of Poincare [French physicist, Jules Henri Poincairè (1854-1912)] , whose influence in this field at that time was very great .... the physical arbitrariness of the theory was less impressive than the mathematical completeness with which it made the Maxwell-Lorentz electromagnetic equations tenable in spite of the menace of the experiments. [p.116] [The impetus for the theory might be more fundamentally described as an effort to save heliocentric and acentric models of the solar system.]
But we shall not understand the position at all unless we realise that, from 1904 until the eclipse observations of 1919 that brought Einstein's general relativity theory to everyone's notice, 'the theory of relativity' meant, to almost all concerned, Lorentz's theory .... [p.116] [In fact the results of the 1919 eclipse observations were, as a test of general relativity theory, statistically insignificant and mathematically ill-conceived. (Click here for more.) Dingle observes later in the chapter that the best that can be said for the general theory of relativity is that it had at the time of writing not been conclusively disproven. [p.122]
Jewish mathematician Hermann Minkowski (1864-1909) provides the surreal "space-time" mathematics that would become a chief characteristic of special relativity mythology thenceforward:
[Minkowski's] distinctive feature, among the few to whose notice the work of both [Lorentz and Einstein] had come, was that he regarded Einstein's presentation of the theory as the one to be preferred, and that precisely because he was a mathematician and not a physicist. He gave yet another form to the general complex of ideas which later became known as the special theory of relativity, and this must be given special notice here, not only because it provided Einstein with the type of mathematical machinery which he was to use in his later general theory, but also, and chiefly, because it contributed perhaps more than any other single factor to the transformation of mathematics from the servant into the master of physics, and introduced more false ideas into the subject - pre-eminently the totally irrelevant idea of time (eternity) - than anything else. It is to Minkowski that we owe the idea of a 'space-time' as an objective reality - which is perhaps the chief agent in the transformation of the whole subject from the ground of intelligible physics into the heaven (or hell) of metaphysics, where it has become, instead of an object for intelligent inquiry, an idol to be blindly worshipped. [p.118]
Reduced to its essence, Minkowski's paper is a piece of pure mathematics .... He takes (quite arbitrarily, if we regard his paper as sui generis as it claims to be) a particular mathematical expression,
c2t2 - x2 - y2- z2 = 1
(which I will reduce to c2t2 - x2 = 1 for simplicity, since y and z play no part in the development of the work but merely give plausibility to the claim that the mathematics has a necessary physical significance) and shows that it is invariant to the transformation of co-ordinates already known as the Lorentz transformation. He gives also a very felicitous geometrical representation of the algebra, which has greatly simplified the task of giving the work a presentable form. [Though it does give the ideological contortionism of special relativity "space-time" something of a presentable form, the American astronomer, Professor Charles Lane Poor (1866-1951), demonstrated that when the invariant "space-time interval" (c2t2 - x2) is converted to the standard Pythagorean invariant form of real-world Euclidean geometry, a complex (imaginary) number (i) is revealed in the time(t) or distance(x) co-ordinate: (c2t2i + x2 or x2i + c2t2), showing that so-called "space-time" geometry, while certainly a mathematical curiosity, has no correlation in physical reality, and thus no place in physics. Poor notably described Einstein as a "confusionist".] [p.118]
The return to mediaeval scholasticism, against which the protest of Bacon and the other pioneers of modern science was thought to have been finally successful, was now complete. With Minkowski's work physics had escaped from experiment and been captured by mathematicians. [p.119]
On the arbitrariness and detachment from physical reality of Minkowski's mathematical speculations:
[Minkowski] takes - quite arbitrarily, of course, in these circumstances - one of an infinite number of mathematical expressions (he might as well, of course, have taken, say, x - ty2/z or any other), and finds the transformation of symbols to which it is invariant. [c2t2 - x2 = 1 is invariant to the Lorentz transformations.] Mathematically the symbols are just symbols and nothing else. He then says, again entirely arbitrarily, 'Let x, y, z be rectangular co-ordinates for space, and let t denote time... The multiplicity of all thinkable x, y, z, t, systems of values we will christen the world.' Why? Why should not a mathematician .... equally well say, 'Let x denote pressure, y volume, z specific heat, and t temperature', then choose some combination of them, and announce laws of thermodynamics which would save the physicists the trouble of making observations? [p.119]
Never before in physics - not even in the theories of Lorentz and Einstein - had x, y, z denoted space or t time (eternity); they had meant respectively place and time (instant). In no application of any formula of physics, and in no co-ordinate diagram, does any co-ordinate have the significance of an indefinitely extended continuum, for the simple reason that all the formulae and diagrams represent relations between what can be observed, and space and time (eternity) cannot be observed ....
Hence, when Minkowski let x, y, z represent space, and t, time (eternity), he was doing something quite unrelated to physics, and his famous conclusion, 'Henceforth space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality', is utterly unwarranted: it is a conclusion about things not dealt with in physics, drawn from a purely gratuitous interpretation of an arbitrarily adopted mathematical formula ....
The fact - if it be a fact - that the Lorentz transformation is physically significant simply means that, in the expression of the relation between our measurements when we refer them to different co-ordinate systems, the values of x, y, z, t are associated with one another and are not such that t always remains separate from the others. That no more means that space and time (in any sense) are arbitrary parts of a single absolute whole than the fact that pressure and volume do not change independently when the temperature is altered means that pressure and volume vanish to shadows, and only a union of the two has objective existence .... [p.120]
.... in much modern cosmology, those who speak of 'space-time' naively imagine that it refers literally to something existing objectively, and so deceive themselves and others into thinking that the world which is the world of all of us has an esoteric quality that only the specially gifted can understand. [p.121]
Tolman [Richard C. Tolman (1881-1948), American mathematical physicist], indeed, many years later told me that when he first read Minkowski's paper his immediate reaction was, 'This is all hooey', and he tossed it aside without further attention. With his excess of modesty he related this as an example of his lack of insight, but I am inclined to give it the opposite interpretation so far as its relation to physics, as distinct from mathematics, is concerned. [p.121]
[Einstein abandons the notion that the velocity of light is constant in vacuo for his general theory. The fact that this undid anything special relativity claimed to do in terms of explaining Michelson-Morley goes conspicuously unchallenged for the most part even to this day.]
.... what [Einstein] did in his so-called general relativity theory was to generalise the relativity postulate alone, and then construct a law of motion of bodies that included their motions under their mutual gravitational influence, and held good for all systems of co-ordinates, in accelerated as well as uniform motions .... it had the serious disadvantage of destroying the possibility of preserving the reconciliation with electromagnetism, which the special theory had claimed for uniform motions. The generalisation of the relativity postulate had the consequence that the other postulate - that of the constancy of the velocity of light, as it is generally called - could no longer be maintained. 'It will also be obvious,' wrote Einstein at the beginning of his 1916 paper, 'that the principle of the constancy of the velocity of light in vacuo must be modified.' [p.122]
The matter, however, is not important for our present purpose, except insofar as it does give some support - very far indeed from proof - for the view that the error in the special theory does lie in the postulate of constant light velocity, for Einstein's theory of gravitation does have some support - again very far from proof - from observation, and nothing is so far known fatally at variance with it. [p.122]
On the conflation of the Lorentz theory, special relativity and Minkowski's ideas of "space-eternity", and the subsequent confusion:
The 'relativity' theory was ascribed to Lorentz, Einstein and Minkowski as though these all contributed to the same set of ideas. The facts that Lorentz's theory was impossible without an ether and Einstein's impossible with one, that Lorentz and Einstein never thought of time as relating to anything but instants and durations while Minkowski never thought of it as relating to anything but 'eternity', that the basic idea of Minkowski was 'space-eternity', which meant nothing whatever in the original papers of either Lorentz or Einstein - all these differences were completely obscured by their unholy alliance under the one word 'relativity'. Phrases like 'time dilation', which meant nothing to anybody, were freely used to describe 'Einstein's special relativity theory', and 'time' and 'space' were declared to be interchangeable .... so that even those who took the trouble to look up Einstein's 1905 paper and found there nothing to which they could possibly attach such notions, became convinced that what normally they would have understood without any difficulty at all must contain some mysterious essence which they were incapable of apprehending, The net result was that they gave up the attempt to understand the matter and submitted to the uncritical acceptance of 'Einstein's special relativity theory' with resignation. [p.123]
Dingle quotes British mathematician and philosopher, A.N. Whitehead (1861-1947):
It is not going too far to say, [wrote Whitehead] that the announcement that physicists would have in future to study the theory of tensors created a veritable panic among them when the verification of Einstein's predictions was first announced. [p.124] [The new tensor calculus which Einstein adopted for the formulation of his general theory of relativity acts as a deterrent to sensible scrutiny by professors disinclined to make the effort to learn the new mathematics. As discussed earlier the "verification" to which Dingle refers is Eddington's 1919 eclipse experiment, though Dingle acknowledges elsewhere (p.122) that the results of this experiment and others with similar purpose were not in fact conclusive. Dingle explains that the problem for many physicists in 1919 was that their introduction to special relativity coincided necessarily with the hype about the general theory in the wake of the 1919 experiment (the special relativity theory had been languishing in more or less obscurity until then), thus conflating the theories in their minds, when in fact they were in many ways incompatible and contradictory.]
.... what is more important than the confusion regarding the authorship or name of the theory is that which surrounded its meaning. Whitehead certainly understood it, and admired without accepting it. Fowler [British astronomer, Alfred Fowler (1868-1940)], though he was prominent in criticising the experimental evidence for the spectrum shift predicted by the general theory, acknowledged that he had not the least idea of what the theory was all about, and those less gifted and less candid showed by their comments that they were quite unaware that the theories of Lorentz and Einstein were essentially different. [p.125]
On Lorentz's assurance to the scientific community and interested members of the public that he really believes in his speculations:
Lorentz, on the other hand, wrote in a special Relativity Number of Nature of February 1921 .... : 'I may remark here that there can be no question about the reality of this change of length ... let there be two rods, I and II, exactly equal to each other ... II will be shorter than I, just as it would be if it were kept at a lower temperature.' This, of course, followed from his own theory of 1904 which preceded Einstein's and ascribed the shortening to an effect of the ether. [p.125]
Dingle pinpoints two ways that questionable aspects of special relativity theory are obscured: firstly by conflating it with the Lorentz theory which allows an ether, and secondly by shifting between claims that calculations or phenomena are subjective "appearances" on the one hand and objective reality on the other:
The general confusion was complete and, as I have said, it has proved the chief means of preserving Einstein's theory, in spite of its obvious untenability, because of the freedom which it allows of switching from Einstein to Lorentz and back as occasion makes convenient. An almost equally effective means of escaping difficulties is the introduction of 'the observer'. When the theory appears to lead to incompatible objective results, they are written off as merely different appearances, but claimed as realities when some actual phenomenon has to be explained .... Is it any wonder that the theory acquired a reputation for unintelligibility when the acknowledged authorities gave such contradictory accounts of what it was all about? [p.125]
The equations worked, so the 'experimenters' became convinced that the theory, whatever it was, must be right. The superior minds acknowledged that they did not understand it, but the majority could not rise to that height. Nothing is more powerful in producing the illusion that one understands something that one does not, than constant repetition of the words used to express it, and the lesser minds deceived themselves by supposing that terms like 'dilation of time' had a self-evident meaning, and regarded with contempt those stupid enough to imagine that they required explanation. Anyone who cares to examine the literature from 1920 to the present day, even if he has not had personal experience of the development, can see the gradual growth of dogmatic acceptance of the theory and contempt for its critics, right up to the extreme form exhibited today by those who learnt it from those who learnt it from those who failed to understand it at the beginning. [p.126]
Dingle summarises:
[Special Realtivity] could not be understood because incompatible ideas, having been given the same name, were regarded as identical; because the essentially physical ideas of the theory were exchanged for metaphysical ideas by a transformation of 'instants' into 'eternity'; and because subjectivity and objectivity were hopelessly mixed up by the conversion of co-ordinate systems into 'observers'. [p.126]
I still think that Einstein's perception of a possible escape from the dilemma of the time a mark of the highest genius, though his failure to see that it could not be actual when it needed such slight additional thought to make that unmistakably evident, reveals all too clearly the limitations of that genius. [There are of course other, less kind interpretations of Einstein's all too convenient and inexplicable blind spots. For example, American astronomer, Professor Charles Lane Poor, famously described Einstein as a "confusionist". Indeed it is difficult not to conclude that Dingle is being over generous or diplomatic. After all, how can it be the "mark of the highest genius" to take seriously something that only "slight additional thought" reveals as nonsense?] [p.127]
Dingle on the essence of prophecy:
It is a question for the specialist now, but in a few decades it will be a matter of universal importance; for the abstract thought of one generation, operating unperceived by the majority, directs the practical activities of the next .... Those who are wise enough to see how the social life of a people is related to its mental state will scarcely contemplate the future with equanimity. [p.127]
If this state of mind exists among the élite of science, what will be the state of mind of a public taught to measure the value of an idea in terms of its incomprehensibility and to scorn the old science because it could be understood? The times are not so auspicious that we can rest comfortably in a mental atmosphere in which the ideas fittest to survive are not those, which stand in the most rational relation to experience, but those which can don the most impressive garb of pseudo-profundity. [p.128]
Dingle draws attention to the misuse of the word "paradox" as a means of masking serious and irresolvable contradiction:
.... the occasion calls for some comments on the most famous problem in the criticism of special relativity, which has constantly arisen throughout its history — the so-called 'clock paradox' or 'twin paradox'. It has been a common and very effective device in this field to avoid the necessity of admitting a contradiction by calling it a 'paradox': it is thereupon automatically regarded by those who do not consider themselves experts in the subject as something to which there is of course an answer, like the paradox of Achilles and the tortoise, which it is not their concern to provide and to which therefore they need pay no further attention. [p.128]
Chapter 9 - The 'Clock (or Twin) Paradox'
Dingle gives the definition of a paradox:
A paradox arises when, from the same premises P, two (or more, of course) apparently contradictory conclusions, X and Y, seem inescapably to follow .... the premises P are the special (or sometimes general) theory of relativity; since the many who have discussed it have differed on the question whether the general theory needs to be brought into the matter, this ambiguity must be admitted: the conclusion X is that, if two similar clocks separate and re-unite and their readings agree at the moment of separation, they will agree at the moment of re-union since the theory allows the motion to be ascribed with equal right to either, and no influence on their readings other than their relative motion can be dealt with by the theory: and the conclusion Y is that one will read an earlier time than the other on re-union, because the special theory of relativity, by virtue of the Lorentz transformation, requires that their rates of working differ. X and Y are obviously contradictory ..... [p.129]
.... nearly everyone accepts Y, on grounds that are almost unbelievably diverse. They involve Doppler effects, observations by external observers in countless varieties of circumstances, the influence of the rest of the universe, electromagnetic considerations, and more ingenious situations than one would have thought possible. They have one thing only in common, apart from their conclusion - they are all unaccompanied by a disproof of X. Had that been given, one would have sufficed; without it their total contribution to the resolution of the paradox is precisely nothing. [p.130]
The commonest attempt to justify the ignoring of X invokes the fact that, in order that 'the clock moved from A to B' shall return to its starting point, it must undergo an acceleration, which removes the problem from the scope of the special theory. But there are three comments that may be made on this. First, Y, like X, is drawn from the special theory, so that if X is nullified by this consideration, so is Y. Second, Einstein at this time evidently considered that the acceleration did not affect the matter, for he wrote: 'It is at once apparent that this result [concerning uniform motion] still holds good if the clock moves from A to B in any polygonal line' .... and it cannot do this without being accelerated. And third, the conclusion X is drawn from the postulate of relativity alone, without the postulate of constant light velocity, and in his general theory Einstein generalised the former postulate to cover both accelerated and uniform motion, so that, if we accept the generalisation, the acceleration cannot invalidate X. [p.130]
Dingle explains that there is no paradox with the Lorentz ether theory:
Consequently, on Lorentz's theory, 'asymmetrical ageing', as Y has been called, would actually occur, and the clock showing the earlier time on re-union would be the one whose velocity through the ether had been the greater. Hence on Lorentz's theory there was no difficulty in disposing of X, because it followed from the postulate of relativity which that theory rejected. [p.130]
The ruses of "appearances" and conflation of Lorentz theory and special relativity are applied by those seeking to resolve the paradox:
A traveller to Arcturus at uniform speed, pictured by Eddington [Arthur Eddington 1882-1944], merely appears to age slowly to an observer on the Earth, and the observer on the Earth likewise appears to age slowly to the traveller, but 'if in some way [the traveller's] motion were reversed so that he returned to the Earth again, he would find that centuries had elapsed here, while he himself did not feel a day older.' Why a retardation of ageing before reversal is only apparent, so that 'really' the traveller ages at the normal rate, and then, having decided to reverse, he regains his lost youth, is explained, according to Eddington, by the claim that the motion 'must be reversed by supernatural means or by an intense gravitational force'. What happens if the traveller reverses by the natural means of suitably operating the engine of his space vehicle is not explained. Needless to say, this was written after Einstein's general theory had re-named 'the relativity theory of Lorentz' as 'the special relativity theory', so that conclusions could be drawn indiscriminately from either, according to what happened to be necessary to preserve it from refutation. [p.131]
I turn now to Einstein's paper on the clock paradox, which, though in one sense it is not an attempt to solve the problem at all but aims merely at showing that the relativity postulate can survive either solution, does dispose of a large number of arguments for solution Y - in particular, all those which attempt to dismiss X by claiming that the effect of the acceleration on reversal invalidates it. [p.133]
Einstein resorts to imagining ad hoc, arbitrary, homogeneous gravitational fields to resolve the paradox. The following is from Einstein's own paper on the clock/twin paradox - see pp 134-136 for the scenario referred to.
Since the change in the reading of U2, judged from K, which might occur during the acceleration of U2 certainly cannot surpass a definite amount, and since U2 works more slowly than U1 during its uniform motion along the line AB (judged from K), then, if AB is sufficiently long, U2 must be behind U1 on its return .... [p.134]
Einstein concedes the obvious:
Even the most loyal adherent of the theory surely cannot maintain that, of two clocks at rest beside, one another, each is behind in time compared with the other. [p.134]
Einstein imagines two reference frames K and K' in which the clock U2 is moving relative to clock U1 in the former, and visa versa in the latter. Again see pp 134-136 for the full description of the scenario Einstein is referring to.
With reference to K' this is explained as follows: It is true that during the stages 2 and 4, the clock U1, moving with velocity v, works more slowly than U2, which is at rest. But this retardation is over-compensated by the quicker working of U1 during stage 3. For, according to the general theory of relativity, a clock works the faster the higher the gravitational potential at the place where it is situated, and during stage 3 U1 is indeed situated in a region of higher gravitational potential than U2. Calculation shows that the consequent advancement amounts to exactly twice as much as the retardation during stages 2 and 4. This completely clears up the paradox, which you have propounded. [p.136] [End of Einstein's paper]
Dingle explains the ad hoc, arbitrary nature of the gravitational fields Einstein imagines into existence to compensate for force applied by the engine of the space vehicle carrying clock U2. Einstein is trying to show that there is no way to distinguish such forces from gravitational forces - the so-called "equivalence principle".
For the one essential characteristic of such a field is that it keeps the clock U2 permanently at rest in spite of the 'external force’, which we may regard as, applied by a traveller carrying the clock. But that traveller can apply the reversing force as he likes - steadily, jerkily, rapidly, slowly, ... - and the gravitational field must therefore also be one of infinite variety. Obviously it is impossible for such a field to be expressible in terms of any independently known quantities at all, as Newton's force was expressed in terms of inertial mass and distance. [p.138]
Even less is it permissible to say what, if any, effect the field necessary in any particular case will have on the rates of the clocks. Einstein says: 'Calculation shows that the consequent advancement amounts to exactly twice as much as the retardation' given by the Lorentz transformation during the uniform motion; but he does not make the calculation, here or anywhere else, and it is obvious that it cannot possibly be done. For it is misleading to call these ad hoc fields 'gravitational fields', since they are essentially different from the fields represented by Einstein's law of gravitation, which are applied to calculate the motions of the planets and such things. Those fields are not ad hoc, and they are related to the distribution of matter in the universe, otherwise they could not be applied to observation, whereas the fields postulated in the 'clock paradox' case are necessarily 'homogeneous', i.e. of the same strength throughout the universe, so that they apply equally to U1 and U2 however far apart they may be. In his 'Autobiographical Notes' Einstein claims that his approach to mechanics is justified 'if one regards as possible, gravitational fields of arbitrary extension which are not initially restricted by spatial limitations'. It is certainly possible to imagine such things, but not to suppose that they 'exist' in the sense in which the field in which the apple falls 'exists', or to call them by the same name. [p.138] [emphasis CG]
Møller [Danish chemist and physicist, Christian Møller (1904-1980)] supposes that the external forces by which U2 is accelerated at the beginning, middle and end of the journey (and therefore the gravitational fields by which they are neutralised when U1 is supposed to move) are all constant and equal to one another. In this 'way certain terms are made to cancel out, and on re-union U2 is indeed found to be behind U1 by the same amount whichever is supposed to move. But all that the traveller with U2 has to do to upset this is to use different forces on starting and reversing. The agreement is then destroyed, and the clock-readings will then reveal which clock has 'really' moved. [p.139]
And, worst of all, even if we allow that the hypothetical fields affect the clock rates in any way at all, that effect would at once enable the motion be ascribed uniquely to one of the clocks. For, if U2 moves there is no field at the reversal of motion, while if U1 moves there is one. Now suppose a third clock U3 at B, stationary with respect to U1 and synchronised with it. Then, if U2 moves, U1 and U3 remain synchronised throughout, but if U1 (and U3 of course) moves, the field that comes into play on reversal puts U1 and U3 out of synchronisation. An observer of U3 from U1 will therefore in due course see it go wrong, so he will know that it is U1 that has moved and that the relativity principle is false. [p.139]
This is specially emphasised by a particular case raised by Lenard as an objection to the general relativity principle, which Einstein claims to have answered in this paper. Lenard imagined a moving railway train brought to a sudden halt by collision with a station buffer. The relativity principle would require that the sudden change of motion could be ascribed either to the train or to the rest of the world, but it is the train that is damaged, not the Church steeple outside the station. Einstein replies, as with the clocks, that we may suppose that the rest of the world has its motion suddenly stopped by a gravitational field, so the relativity principle is preserved. But he does not proceed to the necessary accompaniment of this stoppage (according to his explanation), that then all the previously synchronised clocks of the world go out of kilter, and that fact, if it is observed to occur, fixes the motion uniquely on the rest of the world. [p.139]
Chapter 10 - The Present Position
Bondi 'does not feel able' to give the sentence asked for, but refers me to two published works of his where it is to be found (he does not say in what parts, and I cannot find it there). Temple tells me that I shall find a reply in Synge's book on the theory, but does not say where, and again I cannot find it. Synge himself does not mention his own book, but implies that the answer is in 'relativistic physics', which my expectation of life does not allow me time to explore. McCrea, alone among English speaking people, finds the question 'meaningless'. Science tells me that the answer appeared in that journal in 1957-8, but gives no reference and does not repeat the answer. So it goes on: the answer is everywhere but where it can be found. [p.142]
Dingle restates the postulates of special relativity and the definition of "time" inherent in them:
The postulates are: (1) the postulate of relativity - that nature contains no absolute standard of rest, such as the Maxwell-Lorentz ether, for example, would provide, that would enable a unique state of uniform motion to be ascribed to a single observable body; (2) the postulate of constant light velocity - that the velocity of light, with respect to any chosen standard, has a constant value c which is independent of the state of (uniform) motion of the source from which it is emitted; i.e. that if, from two sources in uniform relative motion, light pulses are emitted in the direction of motion at an instant at which the sources are adjacent to one another, those pulses will thereafter remain adjacent and reach a distant point at the same instant. The definition is that the time (instant) of an instantaneous event, occurring at a distance r from a clock which is accepted as a standard (r being measured by a standard scale at rest with respect to the clock) is given by subtracting r/c from the clock reading when a light-pulse, emitted at the time (instant) and place of occurrence of the event, reaches the clock.
It should be observed, however, that if, according to pre-relativity kinematics, which in this respect was never questioned by Einstein, we define the velocity of a uniformly moving body as the distance it covers in unit time (duration), the definition follows from the second postulate, so the incompatibility of the theory lies between the two postulates alone. [p.142]
Dingle explains British mathematician, Edmund Whitaker's (1873-1956) concept of a "postulate of impotence":
A postulate of impotence, [writes Whitaker] is not the direct result of an experiment, or of any finite number of experiments; it does not mention any measurement, or any numerical relation or analytical equation; it is the assertion of a conviction, that all attempts to do a certain thing, however made, are bound to fail. We must therefore distinguish a postulate of impotence, on the one hand, from an experimental fact: and we must also distinguish it, on the other hand, from the statements of Pure Mathematics, which do not depend in any way on experience, but are necessitated by the structure of the human mind; such a statement as, for instance, 'It is impossible to find any power of two which is divisible by three'. We cannot conceive any universe, in which this statement would be untrue, whereas we can quite readily imagine a universe in which any physical postulate of impotence would be untrue. [p.143]
Dingle holds that Einstein's rejection of the ether is a "postulate of impotence":
We note only that Einstein's first postulate (not the whole of his theory), is a direct example of Whittaker's postulates, which has been not very happily expressed as 'It is impossible by any experiment to detect uniform motion relative to the aether.’ .... Einstein's postulate, which he expressed as 'the phenomena of electro-dynamics as well as of mechanics possess no properties corresponding to the idea of absolute rest', implies that the very idea of such an ether is excluded from physics. I think it is still true to say that no phenomenon has revealed itself that would disprove this postulate, so we may continue to use it in our theories so long as we do not forget that it is unprovable and might be false. All we can do is to keep our minds open to the possibility, when we meet with difficulties in interpreting experimental results, that we might have come across a fact that destroys it. [p.144] [In fact, the ether theory has never really been completely abandoned, though some physicists prefer to give it a different name now.....]
The second postulate, on the other hand, is directly testable by experiment or observation, and so is open to conclusive proof or disproof. Numerous so-called tests have been made, and have all given results, which have been held to prove the truth of the postulate. The failure to perceive that they are all invalid is, I think, one of the most remarkable examples of the paralysis of the intellect by which physics has been afflicted through the abandonment by the 'experimenters' of the use of their intelligence and their submission to the dictation of 'mathematicians', for the invalidity of these 'tests' is so easy to see when one looks at them with an unprejudiced mind that it could not possibly have been overlooked by anyone of even moderate intelligence had he used that modest gift. [p.144]
Dingle shows that de Sitter's double star observations, cited often as confirmation of the second postulate of special relativity, do not rule out the non relativistic possibility that light travels at c with respect to its source:
The maximum discrepancy, therefore, between emission-intervals and arrival intervals is 1 minute - exactly the same as on Einstein's postulate, so these observations tell us precisely nothing to enable us to choose between Einstein's postulate (which is, of course, that of the Maxwell-Lorentz electromagnetic theory) and the postulate that light keeps a constant velocity with respect to its own source (which was proposed in 1908 by Ritz [Swiss physicist Walther Ritz, (1878-1909)] as an alternative to the Maxwell-Lorentz view, but he died before de Sitter's argument was conceived). [p.145]
Although de Sitter's argument may be regarded as, in a sense, the canonical observational 'proof' of Einstein's second postulate, there have been a large number of others in more recent times, which it is unnecessary to consider individually because they all suffer from the same fatal defect - they involve a circular argument. In brief, though they take various forms, they all involve the assumption, at some stage, of the present electromagnetic theory of light .... All that these 'proofs' can possibly do, I repeat, is to show that if we use the present electromagnetic theory of light, we must supplement its equations by those of the Lorentz transformation in order to get agreement with experiment. They cannot throw any light at all on the truth or falsity of either the electromagnetic theory of light or the special relativity theory. [p.146] [emphasis CG]
On the circular argument inherent in the aforementioned "meson" experiment as a test for the time dilation:
It would be too complex a task to trace out in detail how the original calculations of the times taken by the particles in question to reach the Earth (which do not accord with observation) would be impossible without using the electromagnetic equations of which Einstein's second postulate is a necessary feature, but it is a matter about which there is no question or possibility of controversy. [p.146]
Dingle's suggests an experiment to test the validity of the second postulate of special relativity which holds that the speed of light c is constant and independent of the speed of its source.

A and B are two sources of light (visible, material sources, not hypothetical particles) of which B is moving rapidly to the left while A is at rest, the paper being the standard of rest. At the instant at which they are adjacent to one another they emit pulses of light towards C and D, which are photographic films whose distances from A are constant and which are moving rapidly downwards through the paper. The relative motion of A and B continues unchanged throughout the passage of the light. If Einstein's second postulate is true the traces on both films will be symmetrically side by side, while if Ritz's hypothesis is true [that the speed of light is dependent on the speed of its source and constant with respect to it], that of the light from A will be above that of the light from B on one film and below it on the other.
Such an experiment would involve no theory at all: the sources would be identifiable unambiguously, the fact of their relative motion would be indubitable, and no measurement of time of passage or assumption about synchronisation of clocks would be involved. It could be done in a vacuum if thought necessary .... The experimental difficulties, of course, might be great, but I have no doubt that they would be overcome readily enough with modern equipment if physicists could rid their minds of the conviction that an experiment to test the postulate is, in Fox's phrase, 'hardly worth doing' [p.148]
.... those physicists - and they are many - who now regard belief in the possibility of an ether as a superstition have simply not learnt the lessons of history, which teach us that discarded ideas have a way of returning to favour. The title of the editorial article in Nature reproduced in the Appendix, 'Don't bring back the ether' (can one imagine Lockyer or Gregory heading an editorial on Rutherford's early hypotheses, 'Don't bring back alchemy'?) [p.149]
.... the Maxwell-Lorentz theory rests on a very limited experimental basis, which we tend to imagine much larger than it is because we misinterpret theoretical requirements as facts of observation. This is particularly so with regard to velocities: we think we have reached velocities approaching that of light when we have, in fact, only inferred them theoretically as possessed by theoretically inferred particles. [p.149]
Dingle discusses the use of new (at the time of writing) radar technology to test special relativity:
There is, however, possibly a scarcely less definitive means of testing the postulate now available by radar observations of the planets .... we have a different means now of observing the nearer planets, namely, by the reflection of radar beams emitted from the Earth, so that we have two independent ways of determining the position at any instant (and therefore of the whole orbit) of, say, Venus - by visual light emitted by the Sun and reflected by Venus, and by radar beams (which, so far as velocity is concerned, we are entitled to assume equivalent to light) emitted from the moving Earth and reflected back to it from Venus. In both cases we have to assume velocities for the radiation concerned, and these will certainly be different on the Einstein and Ritz theories, though exactly what the difference should be is uncertain because of uncertainty in what velocity a valid theory containing the Ritz hypothesis would require of reflected light. [p.150] (see also p.151)
On the perihelion of Mercury as a "proof" of general relativity:
.... the strongest point in favour of Einstein's theory is its explanation of the orbit of Mercury. If, however, it should turn out that Einstein's second postulate has to be abandoned, the revised orbit of Mercury, the fastest moving of the planets, when the actual observations are corrected for the new time of passage of the light, may lead to a revision of the conclusion to be drawn concerning the relative merits of the two theories. [i.e. Newtonian and Einsteinian mechanics] [p.151]
Dingle explains the "Doppler effect":
This, considered purely as a fact of observation, quite apart from its interpretation, is simply a relation between (1) the relative motion, along the line joining them, of a source of light and an observer, and (2) the spectrum of that light as seen by that observer (for 'observer' here we may, of course, substitute 'spectrometer' .... the effect is wholly objective). If source and observer are approaching one another, the spectrum is shifted in one direction (which, without prejudice, we may describe as towards the shorter wave-lengths) and if they are receding from one another, it is shifted in the opposite direction - with respect, in each case, to its position when source and observer are relatively at rest. [p.151]
The only observable difference, then [according to the Lorentz model], between a movement of the source towards the observer and an equal movement of the observer towards the source, is that in the first case observation of the effect is delayed and in the second case it is immediate. Synchronised clocks at the positions of source and observer would therefore reveal unquestionably which of the two has moved. [p152]
It is obvious that questions of the highest importance to cosmology arise from [choosing the special relativity model over the Lorentz one]. It implies, for instance, that the red-shifts now observed in the spectra of the distant nebulae (if they are indeed Doppler effects, which, though it is the universal conviction, is a most hazardous speculation) denote velocities existing now, and not millions of years ago. But that is only one of the numerous examples of the general failure to appreciate the impossibility of accepting both the relativity postulate and assumptions concerning motion and gravitation that are meaningless without a Lorentzian ether .... [p.15]
The fact is that we know far less about these things than we imagine. The more one reflects intelligently on the nature of light, matter and gravitation, the more he realises that there arc problems connected with them that are quite insoluble in terms of our current notions. [p.153]
Back to Part One |
Download the full version of Science at the Crossroads here. And the appendix here.
